GCSE Maths Trigonometry | Trigonometric ratios examples and solutions | Similar triangles trigonometry In this video I will show several examples dedicated to Trigonometric ratios in which we will learn how to determine and label sides of the right angle triangle in order to find unknown element in the triangle. I will show how the transformation of scaling leads to similar triangles and how it is connected with trigonometric ratios.
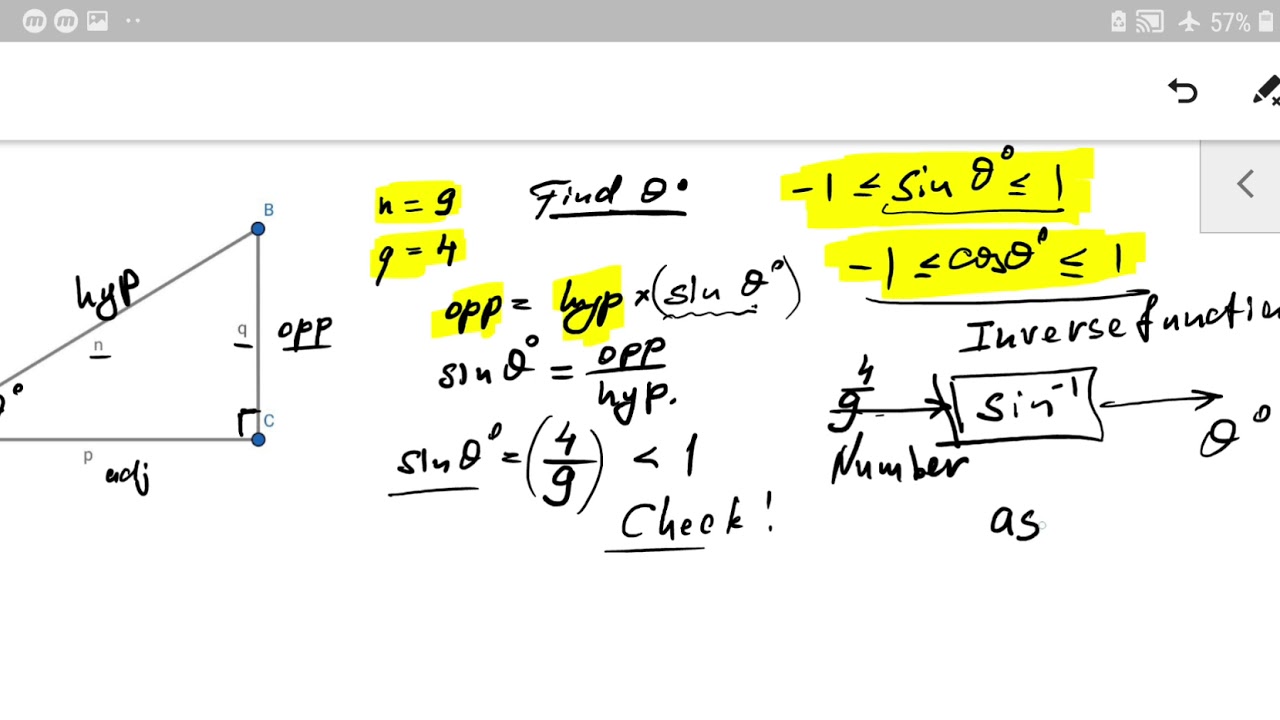
I will also give the checkpoint that allows you to test the correctness of the answer you've got. This is very necessary testing tool that you will definitely apply when sitting exams. Also I will give you the way for proper calculations for angles and for inverse trigonometric functions that will ensure you that you are doing all correctly during ratios rearrangements
This is new series of videos dedicated to Trigonometry : GCSE Trigonometry . It doesn't include Further trigonometry, however this series will learn give you the best way ever to memorize trigonometric ratios and also you will learn how to apply it not only to MATH problems but also to Physics and to real life problems.
The playlist covers the following topics within trigonometry:
- Correct Labelling sides of a right angled triangle
- The trigonometric ratios
- Problem solving
- Applied Trigonometry
- How to operate with the unit circle
- True bearings
- 3-dimensional problem solving
Trigonometry is a branch of mathematics that deals with triangles. In particular, it considers the relationship between side lengths and angles in right-angled triangles. We can apply trigonometry everywhere: in engineering, astronomy, architecture, navigation, surveying, the building industry, and in many other branches of applied science.
For the right angled triangle with angle x (Degrees)
the hypotenuse (HYP) is the longest side
the opposite (OPP) side is opposite to the angle x
the adjacent (ADJ) side is adjacent to the angle x
For a particular angle of a right angled triangle the ratios
OPP/HYP, ADJ/HYP and OPP/ADJ are not changing.
These ratios have the traditional names sine, cosine and tangent respectively. We use shortcuts as sin, cos and tan.
Sometimes you need to find angle itself if you are given the ratios. In this case you can use graphics calculator (or GDC) or normal scientific calculator for finding these inverse trigonometric functions. We can define inverse cosine and inverse tangent in a similar way.
I will give you a bit of applications to science: we will discuss Hipparchus approach and actually you might find useful for your internal projects connected with exploration and discovery
Hipparchus was a Greek astronomer and mathematician born in Nicaea in the 2nd century BC. He is considered among the greatest astronomers of antiquity.
Problem 1: How Hipparchus measured the distance to the moon
Problem 2: How Hipparchus measured the radius of the moon
We also consider ANGLES OF ELEVATION AND DEPRESSION
The angle between the horizontal and your line of sight is called the angle of elevation if you are looking upwards, or the angle of depression if you are looking downwards.
When using trigonometry to solve problems we often use:
the properties of isosceles and right angled triangles
the properties of circles and tangents
angles of elevation and depression.
Problem Solving
The trigonometric ratios can be used to solve a wide variety of problems involving right angled triangles.
For optimization:
foundation GCSE, GCSE maths, Math GCSE, iGCSE Maths, Math iGCSE, higher GCSE, GCSE higher tier, GCSE revision, GCSE maths revision, GCSE questions, GCSE problems, Egyptian triangle, right angled triangle,GCSE maths trigonometric ratios,GCSE MATHs trigonometric ratios,GCSE MATHS trigonometric equations, Trigonometry in science, applied trigonometry, inverse trigonometric functions,basic trigonometry,basic trigonometry sin cos tan,math,basic trigonometry for beginners,basic trigonometry lessons,basic trigonometry problems.,trigonometry ratios,trigonometry,trig functions,trig ratios,explained,sin cos tan,sohcahtoa,right triangle trigonometry,finding sides and angles,applications,examples,trigonometry introduction,trigonometry basic introduction,basic introduction,lessons,for beginners, similar triangles,similar triangles geometry,geometry,similar triangles proportions,similar triangles solve for x,similar triangles find missing side,solve for x,missing sides,missing angles,proportions,rations and proportions,enlargement ratio,similar figures and proportions
0 Comments